K-means Clustering and its Cybersecurity Use Cases

What is K-means Clustering?

k-means clustering is an iterative aggregation or (clustering) method which, wherever it starts from, converges on a solution. The solution obtained is not necessarily the same for all starting points. For this reason, the calculations are generally repeated several times in order to choose the optimal solution for the selected criterion. For the first iteration, a starting point is chosen which consists of associating the centre of the k classes with k objects (either taken at random or not). Afterwards, the distance between the objects and the k centres is calculated and the objects are assigned to the centres they are nearest to. Then the centres are redefined from the objects assigned to the various classes. The objects are then reassigned depending on their distances from the new centres. And so on until convergence is reached.

Use of K-means Clustering?

The k-means method is used to divide the observations into homogeneous clusters , based on their description by a set of quantitative variables. k-means clustering has the following advantages in particular: An object may be assigned to a class during one iteration then change class in the following iteration.By multiplying the starting points and the repetitions, several solutions may be explored.

K-Means Algorithm

Conventional k-means requires only a few steps. The first step is to randomly select k centroids, where k is equal to the number of clusters you choose. Centroids are data points representing the centre of a cluster.

The main element of the algorithm works by a two-step process called expectation-maximization . The expectation step assigns each data point to its nearest centroid. Then, the maximization step computes the mean of all the points for each cluster and sets the new centroid. Here’s what the conventional version of the k-means algorithm looks like:

means algo.jpg

The quality of the cluster assignments is determined by computing the sum of the squared error (SSE) after the centroids converge, or match the previous iteration’s assignment. The SSE is defined as the sum of the squared Euclidean distances of each point to its closest centroid. Since this is a measure of error, the objective of k-means is to try to minimize this value.

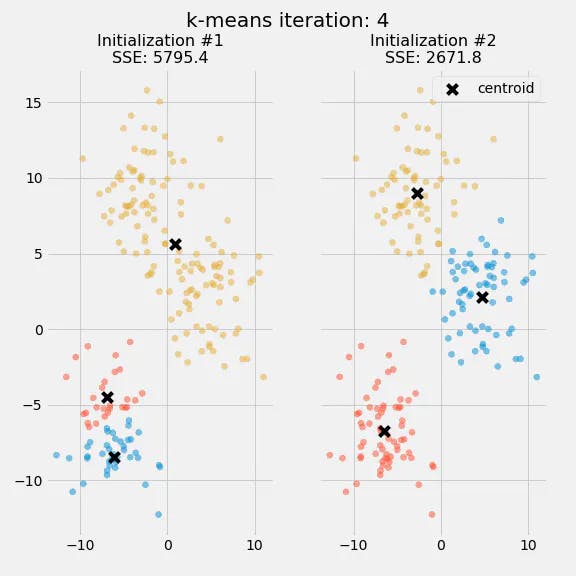
The purpose of this figure is to show that the initialization of the centroids is an important step. It also highlights the use of SSE as a measure of clustering performance. After choosing a number of clusters and the initial centroids, the expectation-maximization step is repeated until the centroid positions reach convergence and are unchanged.

The random initialization step causes the k-means algorithm to be nondeterministic, meaning that cluster assignments will vary if you run the same algorithm twice on the same dataset. Researchers commonly run several initializations of the entire k-means algorithm and choose the cluster assignments from the initialization with the lowest SSE. K-means Clustering Use-Case in Security Domain:-

With the advancement in technology and the increase in the number of digital sources, data quantity increases every day and, consequently, the cybersecurity-related data quantity. Traditional security systems such as Intrusion Detection Systems (IDS) are not capable of handling such a growing amount of data set in real-time. Cybersecurity analytics is an alternative solution to such traditional security systems, which can use big data analytics techniques to provide a faster and scalable framework to handle a large amount of cybersecurity-related data in real-time.

K-means Clustering is one of the commonly used clustering algorithms in cybersecurity analytics aimed at dividing security-related data into groups of similar entities, which in turn can help in gaining important insights about the known and unknown attack patterns. This technique helps a security analyst to focus on the data specific to some clusters only for the analysis. To improve performance, k-means can exploit the triangle inequality to skip many point-centre distance computations, without affecting the clustering results.

It is a fact that log files contain permanent documentation of almost all events that take place in a system, they are frequently used by analysts to investigate unexpected or faulty system behaviour in order to find its origin. In some cases, the strange behaviour is caused by system intrusions, cyber attacks, malware, or any other adversarial processes. Since such attacks often lead to high costs for affected organizations, timely detection and clarification of consequences is of particular importance.

Independent from whether anomalous log manifestations are caused by randomly occurring failures or targeted adversarial activity, their detection is of great help for administrators and may prevent or reduce costs. K-means Clustering is able to largely reduce the effort required to manually analyze log files, for example, by providing summaries of log file contents, and even provides functionalities to automatize detection of anomalous behaviour. K-means in Intrusion Detection

The k-Means clustering algorithm partition a dataset into meaningful patterns. Intrusion Detection System detects malicious attacks which generally include theft information. It can be found from the studies that clustering based intrusion detection methods may be helpful in detecting unknown attack patterns compared to traditional intrusion detection systems. K-means for Malware Detection

To optimize detecting malware in computers and network systems. The genetic K-means algorithm is based on the HMM, enhancement for malware classification uses genetic operators to improve normal K-means. In this, API call sequences that are extracted dynamically and opcode sequences that are extracted statically are used. The evaluation based on the HMM proves that API call sequences are better for malware detection. The proposed clustering algorithm (genetic K-means algorithm) is applied in classifying the malware based on the scoring of the HMM